Ленивые операции над множествами в C++

Введение

В C++ нет понятия “множество”. Есть std::set, но это всё-таки конкретный контейнер. Есть функции для работы с упорядоченными диапазонами: merge, inplace_merge, includes, set_difference, set_intersection, set_symmetric_difference, set_union, но это алгоритмы, они не ленивые, и при вызове сразу вычисляют результат. К тому же они предназначены для работы строго с двумя диапазонами.

Что же делать, если, во-первых, диапазонов много (больше двух), а во-вторых, мы хотим вычислять результат не сразу, а по необходимости?

В данной публикации я хочу показать, как спроектировать ленивый диапазон, который будет производить какую-либо операцию с N множествами.

В публикации Ленивые итераторы и диапазоны в C++ я разбирал, что такое ленивые диапазоны.

Операции с несколькими диапазонами

Для начала определимся с терминологией. Множеством я буду называть диапазон, элементы которого упорядочены. Таким образом, первый элемент множества, задаваемого диапазоном с порядком “меньше”, — это наименьший элемент этого множества.

Все операции с несколькими множествами сводятся к двум этапам:

Продвинуть диапазоны-множества так, чтобы достичь следующего элемента итогового множетсва.
Выбрать один элемент среди текущих элементов всех диапазонов-множеств;

Процесс удобно представлять в виде движущихся входных лент, с которых выбранные элементы переписываются на выходную ленту.

В качестве примера рассмотрим слияние нескольких множеств.

В начале у нас есть три ленты: первая состоит из элементов {1, 2, 3}, вторая — из элементов {2, 3, 5}, а третья — {3, 5, 6}. Текущий элемент каждой ленты — это её первый элемент.

Поскольку нам требуется произвести слияние множеств, то на каждом шаге нужно выбирать наименьший элемент. На первом шаге выбираем элемент 1 на первой ленте и выписываем его на выходную ленту.

Шаг 1

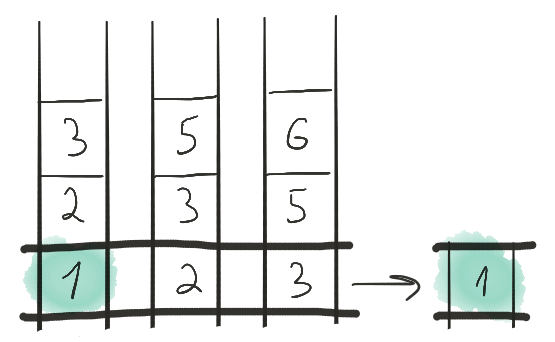
После чего продвигаем первую ленту на один элемент. Затем выбираем элемент 2, снова с первой ленты.

Шаг 2

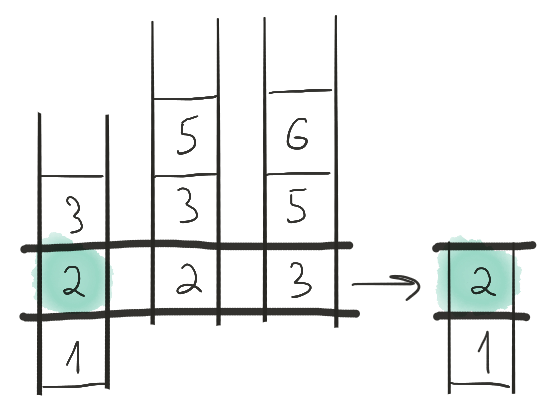
Продвигаем первую ленту. Теперь на первой ленте тройка, а на второй — двойка. Двойка меньше, так что выписываем двойку на выходную ленту, продвигаем вторую ленту.

Шаг 3

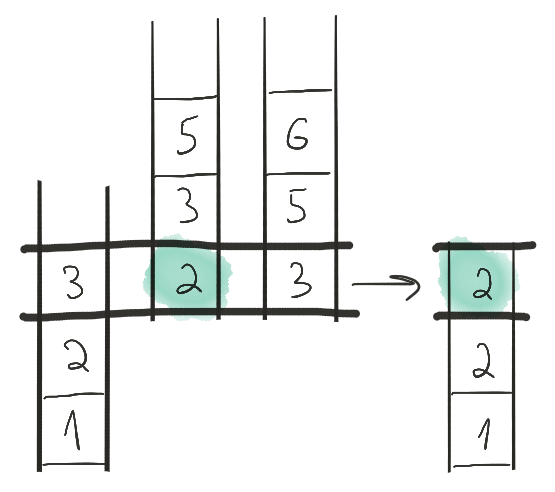
На этом шаге на всех лентах стоят тройки. Выбираем тройку с первой ленты.

Шаг 4

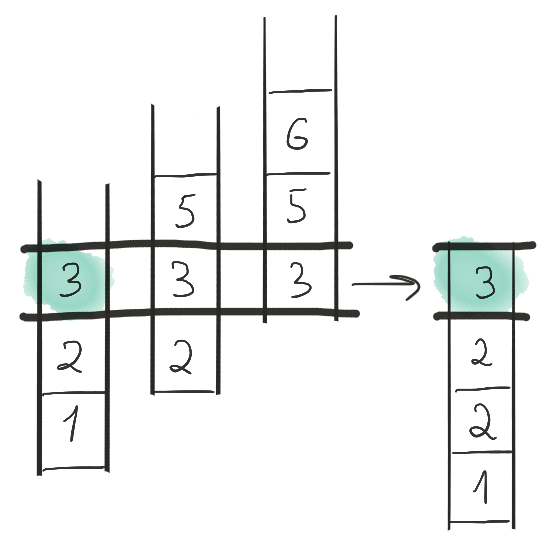
Снова продвигаем первую ленту. После продвижения оказывается, что первая лента закончилась. Это значит, что она выбывает из рассмотрения, и дальнейшие шаги будут произведены только для второй и третьей лент.

Шаг 5

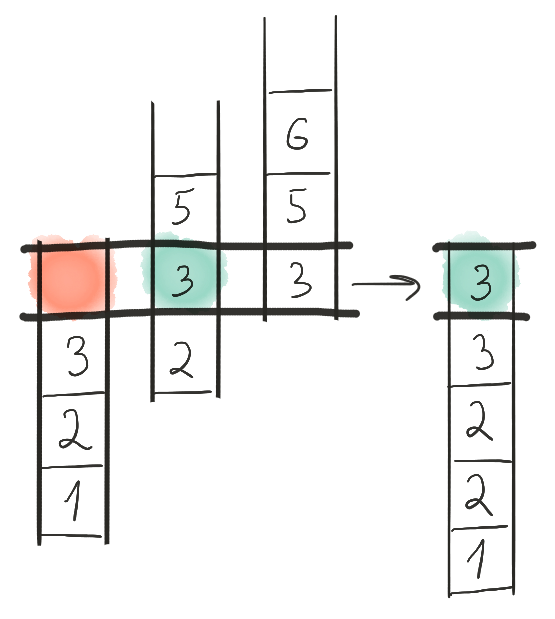
И так далее.

В итоге на выходной ленте будет записано {1, 2, 2, 3, 3, 3, 5, 5, 6}. Что, собственно, и ожидалось.

Мы рассмотрели операцию слияния, однако, нет никаких препятствий для аналогичной реализации объединения, пересечения, симметрической разности и других операций со множествами.

Алгоритм слияния

Итак, общая концепция понятна. Но для того, чтобы написать код, нужен алгоритм. Не будем изобретать велосипед, возьмём классический алгоритм слияния k списков.

Подготовка:

Определим операцию сравнения двух множеств. Множество U будет считаться меньше множества V, если наименьший элемент множества U меньше наименьшего элемента множества V (напомню, что наши диапазоны упорядочены, так что наименьший элемент всегда стоит в начале диапазона);
Пустые множества выбросим из рассмотрения;
Сложим множества в пирамиду (кучу) таким образом, что на вершине пирамиды будет лежать наименьшее множество.

Шаг слияния:

Вынимаем из пирамиды наименьшее множество;
Выписываем наименьший элемент этого множества;
Продвигаем это множество на один элемент вперёд;
Если множество стало пусто, выбрасываем его;
Если множество всё ещё непусто, кладём его обратно в пирамиду.

Таким образом мы выпишем все элементы всех множеств в порядке их неубывания за время O(k + logk * n), где k — количество множеств, n — суммарный размер всех множеств.

В результате можно написать следующий код.

Переложение на итераторы

Из описания алгоритма и кода видно, что он хорошо разбивается на три части:

Предподготовка;
Выбор текущего элемента (он всегда на вершине пирамиды);
Переход к следующему элементу.

И это прекрасно ложится на то, что мы умеем делать с итераторами, а именно:

Инициализация;
Разыменование;
Продвижение.

Поэтому, долго не думая, берём Iterator Facade и делаем свой итератор.

Код итератора тут: Burst Merge Iterator.

Дизайн

Приводить весь код в данной публикации я не буду, но остановлюсь на важных моментах в проектировании итератора слияния.

Базируется на итераторах

Исходные множества, которые мы планируем слить воедино, задаются двумя итераторами, то есть одним диапазоном. При этом каждый элемент этого внешнего диапазона — это сам по себе диапазон, то есть одно из тех множеств, которые мы будем сливать (тут можно вспомнить историю про ленты).

Внешний диапазон должен обладать произвольным доступом (random access range) — именно он и будет выступать пирамидой, которую мы будем переупорядочивать в процессе слияния.

Внутренним же диапазонам достаточно однопроходности (input range), поскольку всё, что с ними происходит — это проверка на пустоту, чтение первого элемента и продвижение на одну позицию вперёд.

Результат — итератор слияния — также будет однопроходным (input iterator).

Быстрое копирование

Итератор должен быстро копироваться. Все стандартные алгоритмы принимают итератор по значению и не стесняются копировать внутри себя.

Поэтому мы поддерживаем “стандартные” свойства итератора, и не храним в нём никаких развесистых структур. В итераторе слияния хранится только только два итератора на внешний диапазон.

Деструктивность по отношению к внутренним диапазонам

То, что итератор слияния не хранит в себе ничего лишнего и быстро копируется, накладывает специфические ограничения. Внешний диапазон, который мы передаём итератору слияния при инициализации, вообще говоря, не владеет контейнерами, которые мы хотим слить, а только ссылается на них. И в процессе работы итератор слияния модифицирует внутренние диапазоны: он же не хранит их в себе, а состояние между вызовами оператора ++ нужно где-то сохранять.

Поэтому для работы итератора слияния нужно создавать отдельное хранилище для внутренних диапазонов, а сами внутренние диапазоны уничтожаются (схлопываются) в процессе продвижения итератора слияния.

Но это не проблема: благодаря этому мы уже получили гибкость и эффективность самого итератора, а организовать красивый интерфейс для обхода явного создания хранилища тоже можно (см. Быстрое создание).

Можно создать диапазон

Итератор-конец для итератора слияния — это не совсем итератор, а ограничитель (sentinel в терминах C++20). Простейший пример такого ограничителя — это ноль для классической сишной строки: у нас нет указателя на конец строки, но мы знаем, что если значение разыменованного итератора равно нулю, то это и есть конец строки.

Это значит, что можно не мучить пользователя, и сразу создавать диапазон, минуя создание отдельных итераторов.

const auto odd = std::vector{1, 3, 5, 7};
const auto even = std::vector{0, 2, 4, 6, 8};

auto range_to_merge =
    std::vector
    {
        boost::make_iterator_range(odd),
        boost::make_iterator_range(even)
    };
const auto merged_range = burst::merge(range_to_merge);

const auto expected = {0, 1, 2, 3, 4, 5, 6, 7, 8};
assert(merged_range == expected);

Код построения диапазона на основе итератора здесь: Burst Merge

Быстрое создание

По умолчанию итератор слияния конструируется из диапазона (см. выше). Но есть и другая возможность.

Можно просто передать кортеж из ссылок на исходные контейнеры:

const auto odd = std::vector{1, 3, 5, 7};
const auto even = std::vector{0, 2, 4, 6, 8};

const auto merged_range = burst::merge(std::tie(odd, even));

const auto expected = {0, 1, 2, 3, 4, 5, 6, 7, 8};
assert(merged_range == expected);

В этом случае библиотека берёт на себя создание и обработку промежуточного хранилища для “технических” итераторов.

Изменяемость

Полученный итератор слияния однопроходен, но есть нюанс: если исходные диапазоны изменяемы, то результирующий диапазон также можно сделать изменяемым. То есть через ленивый диапазон слияния мы можем модифицировать исходные контейнеры:

auto first = std::vector{50, 100};
auto second = std::vector{30, 70};

auto merged_range = burst::merge(std::tie(first, second));
boost::for_each(merged_range, [] (auto & x) { x /= 10; });

assert(first[0] == 10);
assert(first[1] == 5);
assert(second[0] == 7);
assert(second[1] == 3);

Есть адапторы

Для того, чтобы встраивать полученный ленивый диапазон в цепочку вычислений, есть адаптор, совместимый с бустовыми адапторами:

const auto first = std::vector{1, 4, 7};
const auto second = std::vector{2, 5, 8};
const auto third = std::forward_list{3, 6, 9};

const auto square = [] (auto x) {return x * x;};

const auto merged =
    std::tie(first, second, third)
        | burst::merged
        | boost::adaptors::transformed(square);

const auto expected = {1, 4, 9, 16, 25, 36, 49, 64, 81};
assert(merged == expected);

Пример с кодом

Вы спросите: “зачем?!” А я отвечу: для упрощения написания и понимания кода.

Конкретно слияние нескольких упорядоченных диапазонов — довольно полезная операция. С её помощью, например, можно написать внешнюю сортировку.

Полный пример внешней сортировки можно почитать здесь: https://wandbox.org/permlink/xhOjmC3sLPpDw9sL

Заключение

Ленивые операции над множествами — достаточно интересная штука. Можно реализовать слияние, объединение, пересечение, разность, симметрическую разность — в общем, всё, что угодно.

И всё это с сохранением эффективности и достаточно приятного интерфейса.

papers

Публикации